› Research : CBIM :: Brain

›› Reconstructing Spatio-Temporal Atlases Of The Corpus Callosum Using Riemannian Geometry

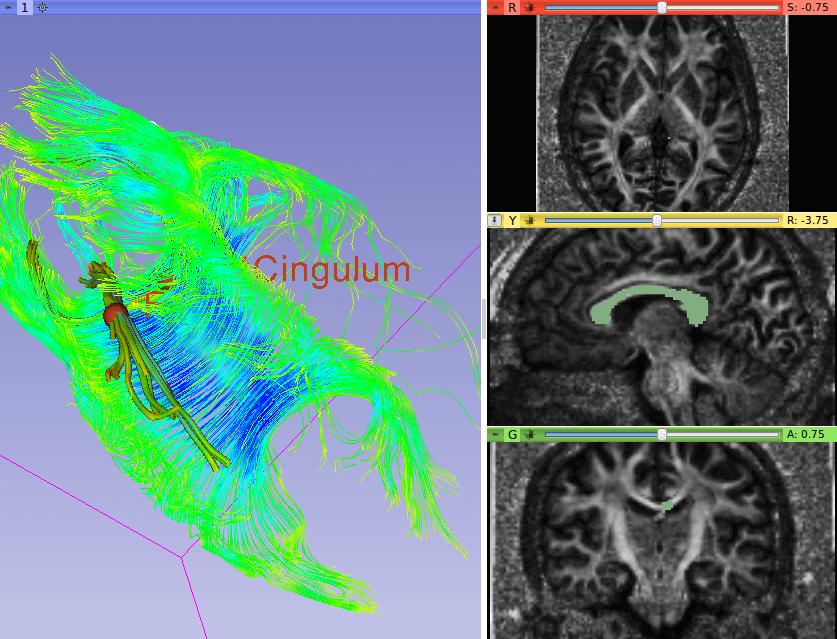
The biological processes underlying the aging of diseased brains can be better understood by identifying how the brain's white matter is composed spatially and how its shape changes over a period of time. Here, we are focusing on the corpus callosum, a part of the white matter that has been directly linked to the prediction and treatment of Alzheimer's disease. We present numerical schemes for reconstructing the dense spatiotemporal atlases of the corpus callosum by processing diffusion tensor images both within and between subjects. The space of diffusion tensors naturally form a curved manifold known as the Riemannian manifold. We develop second-order statistics on this manifold using a Riemannian metric. Results demonstrate that our numerical scheme is more robust in high curvature areas and comply more closely with the known anatomy when compared to other methods that use Riemannian geometry and cost function minimization in linear spaces.